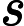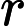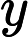Difference between revisions of "Functions composed of Physical Expressions"
From S.H.O.
| Line 11: | Line 11: | ||
<math>\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) = \underset{constant}{\frac{\mu_0\ q'}{4\pi}} \times \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \times \underset{dislocation}{\frac{d\mathbf{r'}}{dt}}</math> | <math>\mathbf{A}\left(\mathbf{r},\mathbf{r'}\right) = \underset{constant}{\frac{\mu_0\ q'}{4\pi}} \times \underset{proximity}{\frac{1}{|\mathbf{r}-\mathbf{r'}|}} \times \underset{dislocation}{\frac{d\mathbf{r'}}{dt}}</math> | ||
| + | |||
| + | ==See also== | ||
| + | |||
| + | * [[The Anatomy of a Physical Expression]] | ||
{{Site map}} | {{Site map}} | ||
Revision as of 00:26, 24 April 2016
Functions for a point charge
The electric scalar potential at due to a point charge at is:
The magnetic vector potential at due to a point charge which had a velocity at is:
See also
Site map
HQ ● Glossary ● April 2016 Presentation
|